'Revisi dramatis bab dasar dalam aljabar': Matematikawan merancang cara baru untuk menyelesaikan persamaan yang sangat sulit
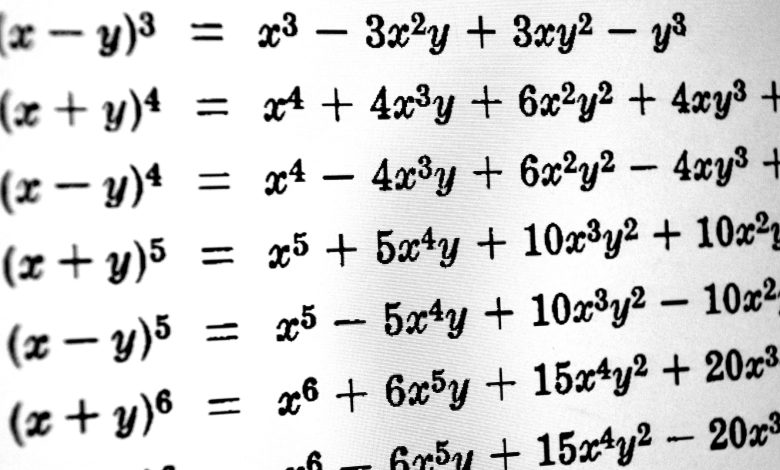
Persamaan polinomial adalah landasan sains modern, memberikan dasar matematika untuk mekanika selestial, grafik komputer, prediksi pertumbuhan pasar dan banyak lagi. Tetapi meskipun sebagian besar siswa sekolah menengah tahu cara memecahkan persamaan polinomial sederhana, solusi untuk polinomial tingkat tinggi telah menghindari matematikawan berpengalaman.
Sekarang, ahli matematika Universitas New South Wales Norman Wildberger dan ilmuwan komputer independen Dean Rubine telah menemukan metode umum pertama untuk menyelesaikan persamaan yang sangat sulit ini. Mereka merinci pendekatan mereka 8 April di jurnal Bulanan Matematika Amerika.
Polinomial adalah jenis persamaan aljabar yang melibatkan variabel yang dinaikkan ke kekuatan non-negatif-misalnya, x² + 5x + 6 = 0. Ini adalah salah satu konsep matematika tertua, menelusuri akarnya kembali ke Mesir dan Babel kuno.
Matematikawan telah lama mengetahui cara memecahkan polinomial sederhana. Namun, polinomial tingkat tinggi, di mana X dinaikkan ke kekuatan yang lebih besar dari empat, terbukti lebih rumit. Pendekatan yang paling sering digunakan untuk menyelesaikan polinomial dua, tiga dan empat derajat bergantung pada penggunaan akar angka eksponensial, yang disebut radikal. Masalahnya adalah bahwa radikal sering mewakili bilangan irasional – desimal yang terus menjadi tak terbatas, seperti pi.
Terkait: Matematikawan baru saja memecahkan masalah berusia 125 tahun, menyatukan 3 teori dalam fisika
Meskipun ahli matematika dapat menggunakan radikal untuk menemukan solusi perkiraan untuk polinomial tingkat tinggi individu, mereka telah berjuang untuk menemukan formula umum yang berfungsi untuk semuanya. Itu karena bilangan irasional tidak pernah sepenuhnya dapat menyelesaikan. “Anda akan membutuhkan pekerjaan yang tak terbatas dan hard drive yang lebih besar dari alam semesta,” kata Wildberger dalam a penyataan.
Dalam metode baru mereka, Wildberger dan rekan -rekannya menghindari radikal dan bilangan irasional sepenuhnya. Sebaliknya, mereka menggunakan ekstensi polinomial yang dikenal sebagai Seri Daya. Ini adalah string istilah yang tak terbatas secara hipotetis dengan kekuatan X, yang biasa digunakan untuk menyelesaikan masalah geometris. Mereka termasuk dalam cabang matematika yang dikenal sebagai kombinatorik.
Para matematikawan mendasarkan pendekatan mereka pada angka Catalan, urutan yang dapat digunakan untuk menggambarkan jumlah cara untuk memecah poligon menjadi segitiga. Urutan ini pertama kali digambarkan oleh ahli matematika Mongolia Mingantu sekitar tahun 1730 dan secara independen ditemukan oleh Leonhard Euler pada 1751. Wildberger dan Rubine menyadari bahwa mereka dapat melihat analog yang lebih tinggi dari jumlah Catalan untuk menyelesaikan persamaan polinomial tingkat tinggi. Mereka menyebut ekstensi ini “geode.”
Geode memiliki banyak aplikasi potensial untuk penelitian di masa depan, terutama dalam ilmu komputer dan grafik. “Ini adalah revisi dramatis dari bab dasar dalam aljabar,” kata Wildberger.



